したっぱプログラマーの日記(The diary of a minor programmer)

『効率が１０倍アップする新・知的生産術-自分をグーグル化する方法-』の巻末のオススメ図書リストに入っていて、何となく読みたかったので、なんとなくパラパラと読んだ。

とりあえず、これから自分の思考の枠組みに入れようと思ったのが、以下の2点。

• ランダムな現象誤認しやすい


• 統計的回帰現象を誤認しやすい

ランダムな現象誤認しやすいってのは、ランダムな現象に「流れ」とか「波」とかいうものを感じてしまうということ。例えば、以下のような16個の数字の列がある。
@ @ * * @ * * * * * * * @ * @ *
これをを見ると、たいていの人は * が多いなぁとか * が連続で出ているなぁといった印象を受けると思う。
これがそれぞれ等しい確率で出てきた文字だとは思わないだろう。
しかし、これは僕が0か1の数字をランダムで出すプログラムを書いて、0だったら @ 、1だったら * 、を出すようにしたもの。

そもそも、確率というのは無限に事象を繰り返すとその値に近づいていきますよ。っていうもの。数十回や数百回のレベルでは偏りが生じることもある。しかし、人間はそのことをあまり自覚できないので、連続して @ が来るとランダムじゃないんじゃないか？という気になってしまう。他にもサイコロの目とか、マージャンの配牌とかいろいろと偏りを感じてしまうことは多々ある。

しかし、まあランダムなんですよっていう話。

統計的回帰現象を誤認しやすいっていうのは、2つの変量が相関関係にあり、その相関が完全ではないときに、一方の変量の両端部分は、もう一方の変量ではより平均値に近い値と対応する傾向があるというもの。
これがどういうことかを下の図を使って説明します。

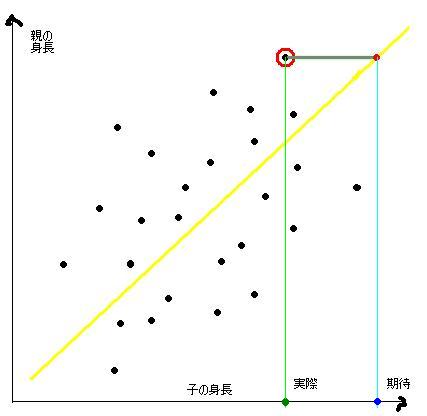
これは僕がテキトーに作ったグラフです。一応、縦軸が親の身長で横軸が子供の身長ということになってます。親の身長が高ければ、こどもも身長が高いことが予想されるので、まあだいたいこんな感じになると思います。親の身長が一番高い点は図の赤丸をつけた点になります。

んで、この点の実際の人を見ると、「うわー、この人でかいなぁ。」ってなるわけですね。んで、「こんだけでかいんだから、子供もさぞかし でかいんだろうなぁ」と思うわけですよ。そのときの期待値が図の青い点ですね。しかし、実際には緑の点ぐらいの慎重なわけです。

これは、両端部分では必然的にそうなってしまうんですね。数学で1番だった人が国語では30位ぐらいだったり、去年の業績が好調だった会社が今年は去年ほど伸びなかったり等々。
不完全だけど相関があるために誤認識してしまうんですね。

以上2つは心に留めておこうと思いました。